This is the translation. The original web-page (oryginalna strona): http://web.engr.oregonstate.edu/~zhange/asymmetric_tensor.html
Eugene Zhang, Harry Yeh, Zhongzang Lin, oraz Robert S. Laramee
Transakcje IEEE dotyczące wizualizacji i grafiki komputerowej, tom 15(1), 2009, s. 106-122.
Papier (PDF, 4.84 Mb).
Niniejszy materiał jest oparty na pracach wspieranych przez Narodową Fundację Naukowa w ramach Grantu nr. CCF-0546881.
Wszelkie opinie, ustalenia i wnioski lub zalecenia wyrażone w tym materiale są opiniami autorów i niekoniecznie odzwierciedlają poglądy Narodowa Fundacja Naukowa (NSF).
Streszczenie
Gradient pola wektora prędkości jest asymetrycznym polem tensorowym, które może zapewnić krytyczny wgląd, który jest trudny do wywnioskowania z tradycyjnych technik wizualizacji pól wektorowych opartych na trajektorii. Opisujemy struktury w wartości własnej i pola wektorów własnych tensora gradientu oraz sposób wykorzystania tych struktur do wywnioskowania zachowania pola prędkości, które może reprezentować albo ściśliwy przepływ 2D, albo rzut ściśliwego lub nieściśliwego przepływu 3D na dwuwymiarową rozmaitość.
Aby zilustrować struktury w asymetrycznych polach tensorowych, wprowadzamy pojęcia rozmaitości wartości własnych i rozmaitości wektorów własnych. Koncepcje te dają szereg teoretycznych wyników, które wyjaśniają związki między symetrycznym a składowe antysymetryczne w polach tensorowych. Ponadto te rozmaitości w naturalny sposób prowadzą do podziału pól tensorowych, które wykorzystujemy do projektowania skutecznych strategii wizualizacji. Co więcej, nieustannie rozszerzamy wektory własne na złożone dziedziny, które nazywamy pseudowektorami własnymi. Korzystamy z równomiernie rozmieszczonych linii tensorów podążających za pseudowektorami własnymi, aby zilustrować lokalną linearyzację tensorów wszędzie wewnątrz złożonych domen jednocześnie.
Zarówno rozmaitość wartości własnych, jak i rozmaitość wektorów własnych są obsługiwane przez reparametryzację tensorów o znaczeniu fizycznym. Pozwala nam to powiązać naszą analizę tensorową z wielkościami fizycznymi, takimi jak obrót, deformacja kątowa i dylatacja, które zapewniają fizyczną interpretację naszej analizy pola wektorowego sterowanej tensorami w kontekście mechaniki płynów.
Aby zademonstrować użyteczność naszego podejścia, zastosowaliśmy nasze techniki wizualizacji i interpretację do badania Sullivan Wir, a także danych symulacji obliczeniowej dynamiki płynów.
Figury
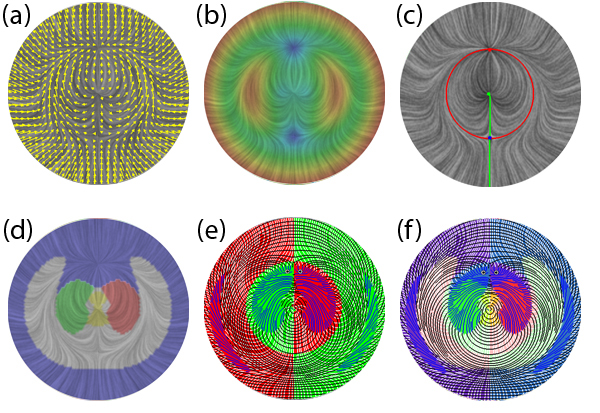
1. Techniki wizualizacji przepływu oparte na wykresie strzałkowym (a), wielkości pola wektorowego (b), topologii pola wektorowego (c) i naszych technikach tensorowych: segmentacja oparta na wartości własnej pokryta wizualizacją pola wektorowego (d), analiza wektora własnego, gdzie kolor wskazuje domeny rzeczywiste i złożone (e) oraz analizę wektora własnego pokrytą analizą wartości własnej (f). Wizualizacja przepływu oparta na tensorach zapewnia dodatkowe i uzupełniające wglądy w pole przepływu.
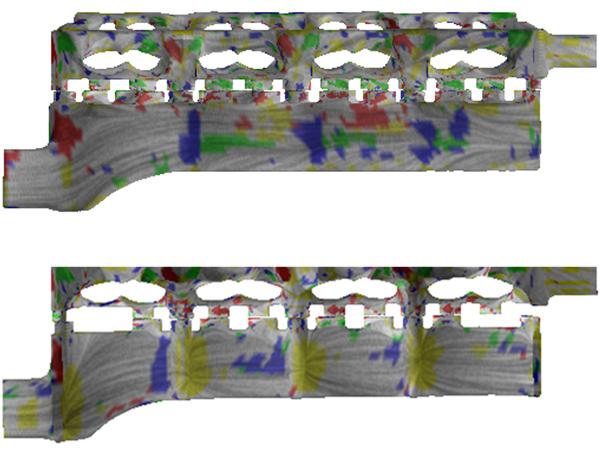
2. Symulacja silnika diesla przy użyciu metody opartej na wartości własnej (po lewej) i metody hybrydowej (po prawej).

3. Nasza technika jest stosowana do danych symulacji płaszcza chłodzącego. Zauważ, że przepływ i geometria są niezwykle złożone.