This is the translation. The original web-page (oryginalna strona): http://www.math.stonybrook.edu/~tony/mazes/otherapps.html
Przez labirynty do matematyki
W tym samym czasie (1986-88) badałem numery labiryntu {M(n) = liczba różnych S.A.T. labirynty z n poziomami} inni ludzie w różnych częściach świata myśleli o tym samym problemie matematycznym.
V. I. Arnol’d
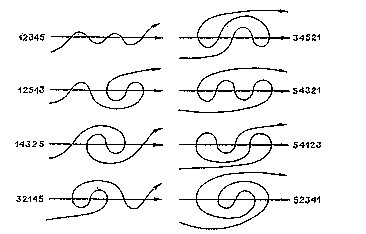Identyczny problem z liczeniem zaproponował V.I. Arnol’d w Moskwie; jest to związane z jego pracą, która ukazała się w Siberian Mathematical Journal z września i października 1988 roku. Arnol zdefiniował meandry jako połączoną, zorientowaną, nie przecinającą się krzywą, która przecina ustaloną zorientowaną linię w kilku punktach. Jego artykuł zawiera tę figurę, która, jeśli jest przechylona w prawo, pokazuje dokładnie osiem ścieżek labiryntu o głębokości 6, a jego M5 to labirynt numer M(6). Arnol’d podaje pierwsze szesnaście „meandrujących liczb”, aż do M16 = M(17) = 252939.
Vladimir A. Kazakov – Ivan Kostov
Mniej więcej w tym samym czasie obliczenie M(n) pojawiło się w innym kontekście, tym razem przy obliczaniu całki macierzy powstającej w kwantowej teorii pola. Dowiedziałem się o tej pracy od Aleksandra Zvonkina, któremu dziękuję za korespondencję. Później on i Lando opublikowali opis tej pracy w artykule z 1993 roku.
Warren Smith
Wystąpiło inne jednoczesne i całkowicie niezależne wystąpienie tego problemu. Warren Smith, pracując nad nowym, podwykładniczym algorytmem komiwojażera w swojej praca z Princeton z 1988 roku, zdefiniował jt(N) jako liczbę topologicznie różnych sposobów, w jakie krzywa Jordana może przecinać zorientowaną linię w płaszczyźnie w dokładnie 2N punktach, i obliczono w górę do jt(10) = M(20) = 8152860.
Tony Phillips
Wydział Matematyki SUNY Stony Brook
tony at math.stonybrook.edu
12 marca 1997
6 kwietnia 1999