This is the translation. The original web-page (oryginalna strona): www.ams.org/publicoutreach/fea
Tony Phillips
Maszyny zrobić Szycia żartem jednym oo Cudów 19 Wieku Wynalazek Mechanicznego. (Mahatma Ghandi żartem powiedział zrobić nazwał go “jednym z kilku przydatnych Rzeczy, Które kiedykolwiek wynaleziono”). W przeciwieństwie do maszyny do pisania i kasy, nie może być przemieszczona przez elektronikę, ponieważ manipuluje materiałem, a nie informacjami. W tej kolumnie zajmuję się matematycznymi aspektami działania maszyny do szycia i często stosowanej nawijarki szpulki: jak topologicznie możliwa jest stebnówka i jak krzywka ukształtowana zgodnie ze spiralą Archimedesa zapewnia równomierne nawinięcie nici na długich szpulkach.
Topologia ściegu
Najbardziej prymitywne maszyny do szycia używały pojedynczego wątku i wykonały ścieg łańcuszkowy:
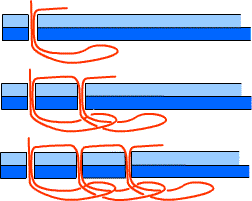
Ścieg: o każdym ściegu, pętli wątku jest ciągnięty przez pętlę, pozostawione przez poprzedniego ściegu. Ta animacja na YouTube pokazuje, jak robi aby maszyna.
Ścieg łańcuszka jest topologicznie nieproblematyczny, ponieważ nici są całkowicie nieobcięte: pociągnięcie za prawy koniec na powyższym obrazku wystarczy do cofnięcia całego szwu. Dzięki temu ścieg łańcuszkowy jest nadal przydatny do zamykania worków z ziemniakami, karmą dla psów lub brykietami z węgla drzewnego, gdzie łatwym rozwiązaniem jest łatwe rozplątywanie. Ale ta cecha jest wyraźnie niepożądana, na przykład w ubraniu.
Pierwsze maszyny, które mogły szyć ścieg blokujący (który nie rozwiąże) zostały wynalezione w latach 1830-1850. Maszyny te używały dwóch nici do szycia szwów.
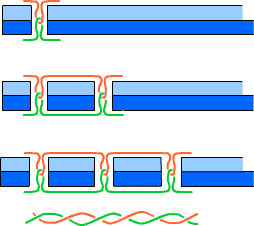
Stebnówka: przy każdym ściegu górna nić łączy dolną, zawsze w tym samym kierunku. Jeśli szmatka zostanie usunięta, nitki mogą być równomiernie skręcone, jeden po drugim, z jednym pełnym skrętem na ścieg.
Na pierwszy rzut oka wykonanie maszyny do stebnowania wydaje się topologicznie niemożliwe. Maszyna używa dwóch nici do szycia szwu; każda nić pochodzi ze szpuli: górna nić ze szpuli umieszczonej w widocznym miejscu na górze maszyny, dolna nić od szpulki, ukryta w środku. Jak to możliwe, aby dwa wątki łączyły się w kółko?
Odpowiedź jest, ze Bębenek Nie jest dołączony zrobić reszty maszyny. W pierwszych maszynach Bębenek siedzi w kształcie pocisku przenoszenia, Który przechodzi wag każdym ściegu, poprzez pętlę utworzoną wag Górnej nici przez pogłębianie ı wycofujące sie Igły. Moze sie do zdarzyć, ponieważ przeniesienie swobodnie przemieszcza sie wewnątrz Urządzenia. W bardziej Nowoczesne Maszyny Bębenek jest schowany w gładkie okrągły przenoszenia metalu, Który pozostaje wag jednym miejscu budowy, chociaż tam pływa niezabezpieczone. Wiec o kazdego ściegu wątek z góry buforu moze Być prowadzony całkowicie Wokół promu, podniesienie Dolnej Nitki w skręcie jako To Jest rysowany Mocno.
Dwie strategie wykonania ściegu blokującego. Po lewej: “Oscylujący (lub wibrujący) prom.” Przy każdym ściegu prom transportujący szpulkę (niebieska nitka) przechodzi całkowicie wokół pętli utworzonej przez górną (czerwoną) nitkę. Po prawej: “Rotary Shuttle”. Szpulka (zielona nić) jest zamknięta w gładkim okrągłym wahadłowcu, który pozostaje nieruchomy, podczas gdy przy każdym ściegu górna nić (żółta) jest narysowana całkowicie wokół niego. W obu przypadkach, aby było to topologicznie możliwe, wahadło musi swobodnie unosić się wewnątrz maszyny. Te dwie animacje GIF są udostępniane przez Wikimedia Commons; kliknij je, aby uzyskać szczegółowe informacje.
Spirala Archimedesa w nawijarce szpuli dla oscylujących maszyn wahadłowych
Dowiedziałem się o tej funkcji od mojego przyjaciela i kiedyś kolega Enrico Giusti, który wspomniał go w wykładzie w zeszłym miesiącu w „matematica e Kultura” konferencji w Wenecji. Jest to wyjaśnione w ramach wystawy w Ogrodzie Archimedesa, muzeum matematyki on zorganizowany na Via San Bartolo Cintoia we Florencji. Wystawa, na skutek Franco Conti, oparta jest na książce Oltre il compasso: la geometria delle krzywej że Conti i Giusti opublikowanym w 2000 roku nawijacz szpulki nici mechanizm podający prezentowane na tej stronie na stronie internetowej muzeum.
Dla tych, którzy nie znają maszyn do szycia stebnowego, każda maszyna ma zwykle swój specyficzny kształt szpulki, małą szpulkę, która wsuwa się do środka wahadła i przenosi dolną nitkę. Tak więc nić przewidziana na dno, dla każdego konkretnego projektu szycia, musi być szczególnie nawinięta na szpulkę. Maszyny do szycia często mają urządzenie do tego celu, zwykle przymocowane do głównej kolumny, odsuwane od operacji szycia.
Jest to Singer Sphinx Model 27, wyprodukowany w 1910 roku, a ostatnio do sprzedaży w serwisie eBay, z pokazanym z bliska nawijaczem szpulki. Model 27 został zaprojektowany z oscylującym wahadłem. Obraz używany za zgodą.
Szpulki dla wahadłowego promienia wahadłowego musiały być wąskie i długie (około 1,5 cala dla pokazanych tutaj). Obraz z serwisu Ebay, używany za zgodą.
W przypadku krótkich, przysadzistych szpul w obrotowych wahadłowcach, zapewnienie, że nitka nawija na równą głębokość, zwykle nie stanowi problemu; nawijarki na tych maszynach pozwalają na wyrównanie nici (chociaż zaleca się obserwowanie procesu i interweniowanie palcami, jeśli to konieczne). Ale długa, wąska szpulka, taka jak w Modelu 27, nie może się sama zatroszczyć: nić musi być poprowadzona tam iz powrotem wzdłuż szpulki podczas nawijania. Bardzo prosty mechanizm może rzutować ruch obrotowy na tył i przód, ale Conti wyjaśnia, w jaki sposób doprowadziłoby to do naprężenia się nici w pobliżu dwóch końców cewki.
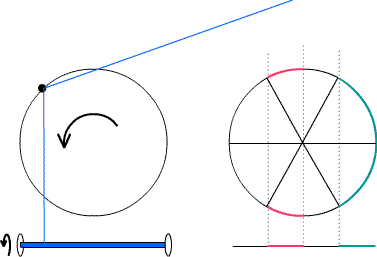
Prosty mechanizm, w którym nitka może być prowadzona przez punkt na obracającym się okręgu o średnicy długości szpuli, a następnie bezpośrednio w dół do szpulki, prowadziłby do stert na końcach. Na diagramie po prawej zielony obszar otrzymałby dwa razy więcej nici niż pomarańczowy obszar tej samej długości.
Rozwiązaniem wymyślonym przez wynalazców i perfekcjonistów maszyn takich jak Model 27 jest użycie obrotowej tarczy jak powyżej, ale zamontowanie na niej krzywki w kształcie dwóch kopii spirali Archimedesa (we współrzędnych biegunowych, r=θr=θ dla 0≤θ≤π0≤θ≤π, i r=−θr=−θ dla −π≤θ≤0−π≤θ≤0). Ramię dźwigni powiększa zakres, aby dopasować długość szpulki.
Działanie nawijacza szpulki na maszynie takiej jak Model 27. Po włączeniu nawijarki gumowa opona (brakująca) spoczywa na głównym kole napędowym. Szpulka jest przytrzymywana przez sprężynowy nurnik po lewej stronie. Gdy szpulka się obraca, napęd śrubowy zazębia się z zębami na krawędzi płaskiego dysku z krzywką w kształcie serca. Gwint jest prowadzony przez wycięcie na końcu ramienia dźwigni, które jest przytrzymywane przez sprężynę przeciw krawędzi krzywki. Po lewej stronie kątowe położenie krzywki jest bliskie θ = π, a nić zostanie przesunięta na lewy koniec cewki. Po prawej krzywka zbliża się θ = 0, a zwoje nici przesuwają się w kierunku prawego końca. W międzyczasie, gdy krzywka obraca się, koniec dźwigni porusza się równomiernie (bezpośrednio proporcjonalnie do θ), z jednej strony na drugą. Obrazy z listy przedmiotów sprzedanych ostatnio w serwisie eBay, używanych za zgodą.
Wreszcie aby zobaczyc nawijarki w akcji, polecam Lizzie Lenard Poradnik “Jak wiatr szpuleczek Długa maszyna zrobić Szycia Singer i załadować transferu wagowo prawidłowy sposób” na YouTube.
Stosowanie spirali Archimedesa zrobić przekształcenia liniowego Ruch jednostajny Ruch kołowy jest opisany w 507 Ruchy mechaniczne przez Henry T. Brown (redaktor “American Artisan”), brązowy, Coombs, Nowy Jork, 1868. Książka jest teraz Dostępne Internecie Niektórych z ruchów Animowanych (nie dziesiątce Jeden). Szczególności Ruch Ten jest nr 96, przedstawione i wyjaśnione poniżej. Tekst daje prosta metode graficznego rysunku Parę spirali Archimedesa.
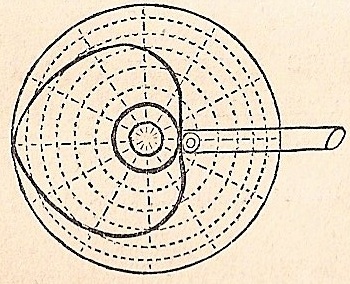96. Kamera z sercem. Jednolity ruch postępowy jest przenoszony na poziomy pręt przez obrót krzywki w kształcie serca. Przerywane linie pokazują tryb wykreślania krzywej krzywki. Długość ciągu podzielona jest na dowolną liczbę części; a od środka opisana jest seria koncentrycznych okręgów. Zewnętrzny okrąg jest następnie dzielony na podwójną liczbę tych podziałów i linii kierowanych do środka. Krzywa jest następnie rysowana przez przecięcia koncentrycznych okręgów i linii promieniujących.
http://www.math.stonybrook.edu/~tony/whatsnew/may15/sewing-machine.html