This is the translation. The original web-page (oryginalna strona): https://www.doc.ic.ac.uk/~mrh/330tutor/ch01.html

Niestety, musisz nauczyć się matematyki na kursie bezpieczeństwa sieci. Gdybyś spojrzał na notatki z kursu, wiesz o co mi chodzi. Bezpieczeństwo pożyczyło wiele narzędzi z matematyki (patrz lista poniżej dla niektórych przykładów) iw pewnym sensie wiele teorii dotyczących bezpieczeństwa można postrzegać jako naturalne postępy matematyki. Dotyczy to szczególnie kryptografii.
- Teoria grup, teoria skończonych Pole, Teoria liczb, geometrii algebraicznej: kryptografia
- Krata Teoria: kontrola dostępu, kryptografia, bezpieczny przepływ informacji
- Teoria prawdopodobieństwa, statystyka: zarządzanie ryzykiem, wykrywania włamań, ochrona prywatności
- Teoria gier: model bezpieczeństwa
- Polityka bezpieczeństwa, weryfikacja i analiza protokołów bezpieczeństwa: Logic
Matematyka pozwala również ludzie formalnie określić i rygorystycznie wykazać bezpieczeństwo. jest to kolejny punkt, dlaczego matematyka jest tak ważna w bezpieczeństwie. Na przykład, jeśli zaprojektował nowy szyfr, jak można mnie przekonać, że szyfr jest bezpieczne?
- Odpowiedź 1: „Nie mogę złamać go, więc musi być bezpieczne” . Nie, każdy może stworzyć szyfr, że on sam nie może złamać. Jednak pytanie brzmi, czy jest ktoś mądrzejszy, kto może go złamać. Kliknij tutaj, aby zobaczyć kilka przykładów szyfrów, które zostały złamane.
- Odpowiedź 2: „Mój szyfr wykorzystuje Klucze xxx-bitowe, wiec jest Bezpieczny”. Nie, Rozmiar klucza nie nie gwarantuje niczego. Trywialny przykład licznik jest szyfrem, Który posiada Znak Budowlany 1024 bitowy Rozmiar klucza i tylko szyfruje tekst jawny przez łamanie tekstu jawnego na kilka 1024 bitowych bloków i XORing Bloki z Kluczem. Szyfr ten ma duzy Rozmiar klucza, pilzner żartem łatwe zrobić złamania.
- Odpowiedź 3: „Nikt nie nie moze odzyskać tekst jawny Dana odpowiadający szyfrogram generowane z mojego szyfru”. Nie Wyobraź Zaprojektowałem szyfr, Który faktycznie pozostawia połowę zwykłego tekstu niezaszyfrowanej. Oczywiscie Nikt nie nie bedzie iść używać w dowolnej Aplikacji. Jednak byłoby na „Bezpieczne”, zgodnie oo definicja, o ile moge zrobić druga połowę zwykłego tekstu Trudno odzyskać.
- Odpowiedź 4: „Nikt nie może odzyskać część tekstu jawnego danego odpowiadający szyfrogram generowane z mojego szyfru”. To brzmi lepiej, jednak wciąż nie jest wystarczająco dobre. Na przykład, niektóre szyfry są deterministyczne co oznacza, że zawsze produkować ten sam szyfrogram dla danego tekstu jawnego i klucz. Może nie być w stanie odzyskać tekst jawny, jednak wiesz, dwa zaszyfrowanych odpowiadać tej samej postaci zwykłego tekstu, jeśli są one identyczne. Do zaszyfrowanych generowane z tych szyfrów, choć ujawniając żadnych bezpośrednich informacji, ujawniają pewne pośrednie informacje o plaintexts.
- Odpowiedź 5: „szyfrogram ujawnia zadných przydatnych Informacji o analogicznym zwykłego tekstu”. Mysle, ze jest do najdalej mozna przejść bez matematyki. Jednak aby, wspólnie dokladnie oznacza „nie ujawniają przydatnych Informacji” oznacza? Mozna zmierzyć informacje W wyciekły przez szyfrogram? Definicja ta nie nie jest zle, ale nieprecyzyjne.
Oto przykład, jak budować i matematycznie szyfr i jak określić i udowodnić zabezpieczeń za pomocą formalnego języka matematyki.
W 1917 Gilbert Vernam wynalazł szyfr do użytku na teleksach. Pomysł jest dość prosty. Po stronie nadawcy każdy przesłany 5-bitowy kod Baudota został zmieszany z losowym 5-bitowym kodem na papierowej taśmie (zobacz poniższy wykres). Po stronie odbierającej kopia taśmy wykorzystywanej w szyfrowaniu służy do odszyfrowania zaszyfrowanego tekstu. Operacją matematyczną używaną w szyfrowaniu i deszyfrowaniu jest XOR (exclusive OR). Klucz ma taką samą długość jak wiadomość i musi być użyty tylko raz.
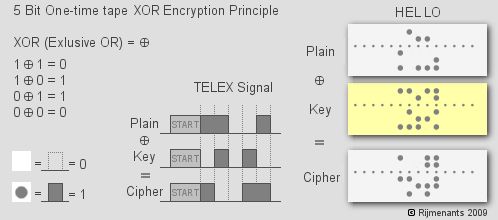
Swoim artykule, Vernam twierdził: Jeśli klucz stosowany w tego typu szyfru jest bardzo długi, tak że nigdy nie powtórzy, a jeśli jakaś część tego klucza nie jest używany przez więcej niż jedną wiadomość, działania „łamanie” szyfru staje się bardzo dużo trudniejsze. Jeśli teraz, zamiast używać angielskich słów lub zdań, zatrudniamy klucz składający się z liter wybranych absolutnie losowo, system szyfrowania jest produkowany, który jest absolutnie nie do złamania. Twierdzenie to jednak było zostawione nieudowodnione aż 25 lat później Claude Shannon wprowadził pojęcie idealnego zachowania tajemnicy i wykazano, że szyfr archiwum Vernam ten poziom bezpieczeństwa.
Więc co jest idealnym tajemnicy? Szyfr jest całkowicie tajne, jeżeli dla każdej wiadomości m i każdy tekst zaszyfrowany c mamy:
Pr [ M = m | C = c ] = Pr [ M = m ]
Jak czytać to równanie? M jest zmienną losową reprezentującą wszystkie możliwe jawne teksty, a C jest zmienną losową reprezentującą wszystkie możliwe teksty zaszyfrowane. Pr [ M = m ] nazywa się a priori prawdopodobieństwo. jest to szacowane prawdopodobieństwo, że tekst jawny będzie konkretną wiadomością m przed zobaczeniem zaszyfrowanego tekstu. I Pr [ M = m | C = c ] nazywa się a posteriori prawdopodobieństwo, które jest szacowanym prawdopodobieństwem, że tekst jawny jest konkretną wiadomością m po stwierdzeniu, że szyfrogram jest c. Intuicja kryjąca się za tą definicją jest taka, że jeśli zaszyfrowany tekst zawiera informacje, które mogą pomóc w odzyskaniu tekstu jawnego, to po poznaniu zaszyfrowanego tekstu będziesz miał większą szansę na określenie tekstu jawnego niż wtedy, gdy nie masz nic. Z drugiej strony, jeśli prawdopodobieństwo nie ulegnie zmianie, otrzymany zaszyfrowany tekst nie zawiera użytecznych informacji o zwykłym tekście. A ponieważ tekst zaszyfrowany nie zawiera użytecznych informacji na temat jawnego tekstu, szyfr jest bezpieczny.
Czy szyfr Vernama jest doskonale tajny? Przed udzieleniem dowodu rzućmy okiem na prostą sprawę, abyś miał intuicyjne przekonanie. Rozważ teraz, że masz tylko jeden bit do zaszyfrowania. Tak więc tekst jawny M może wynosić 0 lub 1. Niech prawdopodobieństwo M=0 być p, wtedy prawdopodobieństwo M=1 jest 1-p. Ponieważ tekst jawny jest tylko jeden bit, w szyfrze Vernama losowo generowany jest jednobitowy klucz. Relację między tekstami jawnymi, kluczami, tekstem zaszyfrowanym i prawdopodobieństwami można podsumować w poniższej tabeli:
| K=0 (0.5) | K=1 (0.5) | |
| M=0 (p) | C=0 (p1 = 0.5p) | C=1 (p2 = 0.5p) |
| M=1 (1-p) | C=1 (p3 = 0.5(1-p)) | C=0 (p4 = 0.5(1-p)) |
Jeśli zaszyty tekst to 0, to tekst jawny może wynosić 0 w przypadku, gdy klucz wynosi 0, lub tekst jawny może wynosić 1 w przypadku, gdy klucz jest równy 1. Podobnie, jeśli otrzymany tekst zaszyfrowany jest 1, wówczas tekst jawny może wynosić 0 w przypadku, gdy klucz wynosi 1, lub tekst jawny może wynosić 1 w przypadku, gdy klucz wynosi 0. Następnie można obliczyć następujące cztery prawdopodobieństwa:
- Pr[M=0|C=0] = p1/(p1+p4) = 0.5p/(0.5p+0.5-0.5p) = p = Pr[M=0]
- Pr[M=1|C=0] = p4/(p1+p4) = 0.5(1-p)/(0.5p+0.5-0.5p) = 1-p = Pr[M=1]
- Pr[M=0|C=1] = p2/(p2+p3) = 0.5p/(0.5p+0.5-0.5p) = p = Pr[M=0]
- Pr[M=1|C=1] = p3/(p2+p3) = 0.5(1-p)/(0.5p+0.5-0.5p) = 1-p = Pr[M=1]
Tak w wypadku jednobitowe szyfr Vernam rzeczywiście spełnia definicji tajemnicy idealne. Ogólne Dowód dla dowolnej długości Vernam szyfr wynika Sam intuicji. Jeśli Sa państwo zainteresowani, mozna iść znaleźć tutaj.