This is the translation. The original web-page (oryginalna strona): http://www.cs.cmu.edu/~bryant/boolean/maps.html
Randal E. Bryant
Don Knuth pracuje nad Tom 4 Sztuka programowania komputerowego. Jeden z rozdziałów dotyczy binarnych diagramów decyzyjnych, BDD, i ich zastosowań, co jest dla mnie bardzo interesujące. Knuth pokazuje, że wiele interesujących problemów graficznych można zakodować jako formuły boolowskie, a wyprowadzony BDD reprezentuje wszystkie możliwe rozwiązania problemu. Często istnieje jakieś kryterium optymalizacji i dość łatwo jest wydobyć „najlepsze” rozwiązanie z BDD za pomocą prostego algorytmu programowania dynamicznego.
Tutaj pokazujemy kilka przykładów, wykorzystując wykres przedstawiający 48 ciągłych stanów, z węzłem dla każdego stanu i krawędzią między dwoma stanami, jeśli mają one wspólną granicę. Po kliknięciu obrazu dla każdej mapy dojdziesz do dokumentu źródłowego w formacie SVG. Oto wykres lokalizujący węzły w stolicach stanów:

Wieże stolicy
Załóżmy, że chcesz odwiedzić stolicę stanu 48 z warunkiem, że każdy stan przejdziesz tylko raz. (Innymi słowy, chcesz znaleźć ścieżkę hamiltonowską na wykresie.) Jak widać z powyższej mapy, jeśli podążasz najbardziej bezpośrednią trasą między stolicami państw, często przechodzisz przez inny stan, lub w przypadku jadąc z Lansing, Michigan do Madison, Wisconsin, przejedziesz przez jezioro Michigan. Zamiast tego powinieneś wybrać najkrótszą trasę jazdy, która pozostaje w obrębie obu stanów dla każdego etapu podróży. Nazwijmy tak ułożyć Wieża stolicy. Oto schemat dopuszczalnych połączeń między krajami:

Na podstawie prostej analizy oraz wysiłków Knutha możemy powiedzieć, co następuje:
- Wszystkie wycieczki muszą zaczynać się lub kończyć w Maine, ponieważ Maine ma tylko jednego sąsiada. Punktem wyjścia będzie Maine.
- Wszystkie wycieczki muszą kończyć się poza Nowym Jorkiem, ponieważ jest to punkt artykulacyjny.
- Istnieje ogółem 68 656 026 różnych wycieczek po stolicy.
Oto najkrótsza wycieczka po stolicy, o łącznej długości 11 698 mil:

Oto najdłuższa trasa stolicy, która wynosi 18 040 mil:

Kolorowanie wykresów
Kolejna interesująca klasa problemów obejmuje kolorowanie mapy. Zasadą jest, że żadne dwa sąsiednie stany nie mogą mieć tego samego koloru. Słynne Twierdzenie o czterech barwach stwierdza, że każdy graf planarny można barwić co najwyżej czterech kolorach.
Ponieważ BDD koduje wszystkie możliwe rozwiązania formuły boolowskiej, możemy łatwo obliczyć, ile jest dostępnych rozwiązań. W przypadku kolorowania wykresów dostosowujemy nasze liczby, aby wyeliminować symetrie z powodu arbitralnego przypisania wartości kolorów (4! Symetryczne przypadki dla 4-kolorowania).
Do barwienia ciągłych 48 stanów istnieje 533,816,322,048 możliwych kolorów. (Jest to 1/2 liczby podanej przez Knutha, ponieważ jego mapa zawiera Waszyngton jako 49. „stan” i może być przypisany do jednego z dwóch kolorów nieużywanych w Maryland i Wirginii.) Oto kilka interesujących przykładów specjalne kolory:
- Zrównoważona kolorystyka, w której każdy kolor jest używany dokładnie w 12 stanach. Istnieje 12 554 677 864 takich barwników, co stanowi zaskakująco wysoką 2,4% wszystkich możliwych barwników.
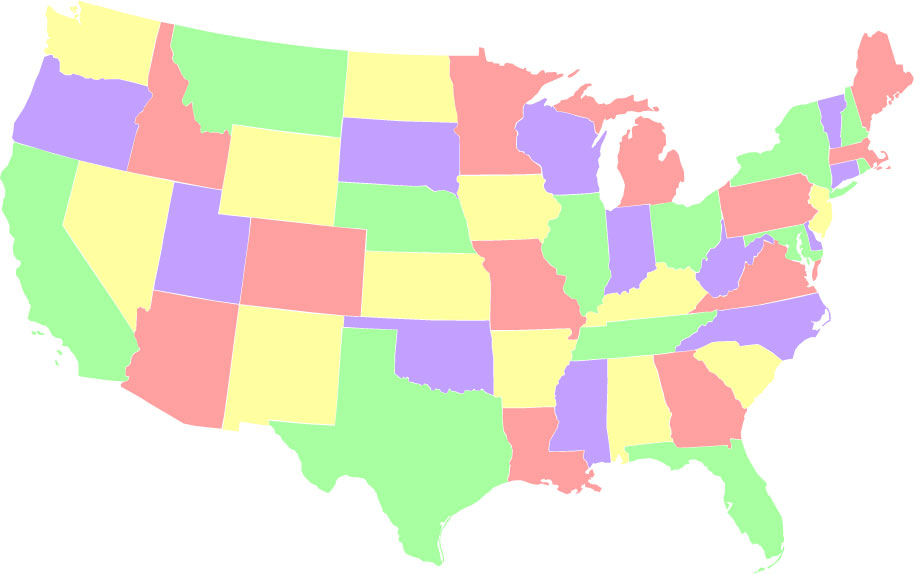
- Niezrównoważone kolorowanie, w którym jeden z kolorów (zielony) jest używany tak mało, jak to możliwe (2 stany). Istnieje tylko 288 sposobów pokolorowania mapy, dzięki czemu jeden kolor zostanie wykorzystany tylko dwukrotnie.

- Niezrównoważone kolorowanie, w którym jeden z kolorów (żółty) jest używany tak często, jak to możliwe (18 stanów). Istnieje 71 002 368 sposobów pokolorowania mapy, dzięki czemu jeden kolor zostanie wykorzystany 18 razy.
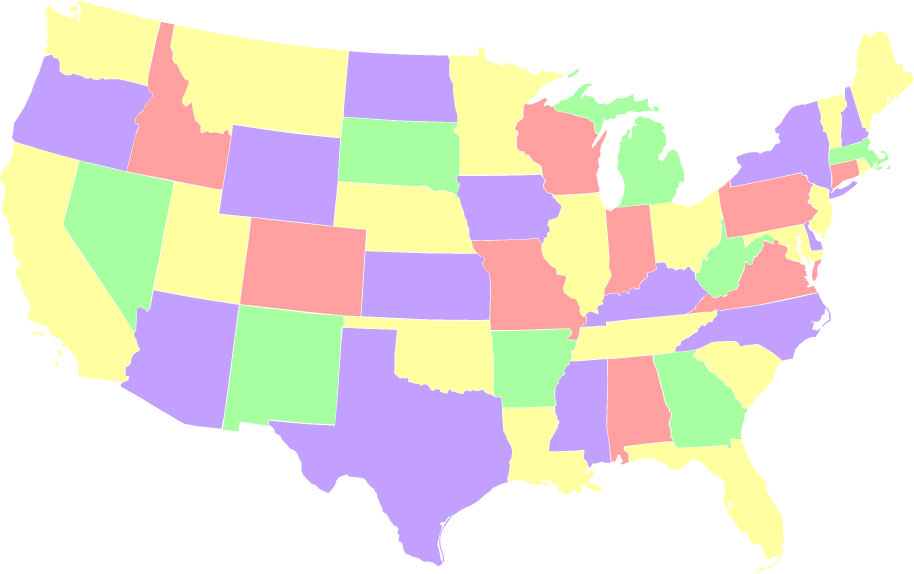
- Łącząc oba. Kolorowanie za pomocą kolorów 2, 13, 15 i 18 razy. Ta sekwencja 1) od lewej do prawej, używa każdego koloru kolejno najmniejszą możliwą liczbę razy, oraz 2) od prawej do lewej, używa każdego koloru kolejno, możliwie największą liczbę razy. Istnieją 24 takie rozwiązania.

Z perspektywy kolorowanie grafu programów, mapa z 48 stanów USA jest dość prosta. Dla bardziej wymagające mapie, patrz strona internetowa o McGregor Wykres.
Randal E. Bryant