Problem kombinatoryczny: Ile jest różnych labiryntów n-poziomowych?

admin

This is the translation. The original web-page (oryginalna strona): http://www.math.stonybrook.edu/~tony/mazes/classify.html

Przez labiryntydo matematyki

Wśród klasycznych i średniowiecznych typów labiryntów są przykłady różnych prostych, naprzemiennych labiryntów tranzytowych o tej samej liczbie poziomów. Na przykład

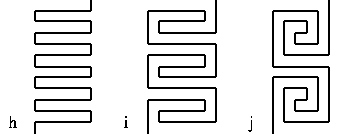
wszystkie te trzy 12-poziomowe ścieżki labiryntu występują. Rodzi to pytanie: ile jest różnych labiryntów o n poziomach?

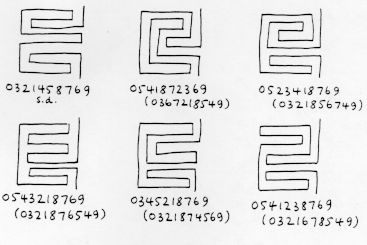
Teraz można wymienić wszystkie możliwe labirynty sat o danej głębokości n, patrząc na wszystkie permutacje 0,…,n i odrzucając te, które nie spełniają trzech warunków, które gwarantują, że sekwencja odpowiada labiryntowi. W rzeczywistości, ponieważ kursy i liczby parzyste nie mogą się mieszać w permutacji, a 0 i n muszą pozostać stałe, wystarczy spojrzeć na wszystkie pary permutacji, jedną z nieparzystych liczb całkowitych 1,…,n -1 (zakładając, że n jest parzyste) i jedną z parzystych liczb całkowitych 2,…,n -2. Na przykład, aby zbudować wszystkie możliwe 8-poziomowe labirynty, należy wziąć pod uwagę pary permutacji 1,3,5,7 i 2,4,6. Takich par jest 24 x 6 = 144, więc można to łatwo zrobić ręcznie. Oto, co można znaleźć dla głębokości od 1 do 8. Na tej liście pominięto nie „interesujące” labirynty (można je zbudować z płytszych labiryntów, dodając trywialne poziomy na górze i/lub na dole). Ten rysunek przedstawia jądra i prostokątne ścieżki labiryntów; losowany jest tylko jeden przedstawiciel każdej pary podwójnej.

Ciekawe labirynty 4,6,7 i 8 poziomów. Losowany jest tylko jeden przedstawiciel każdej pary podwójnej.
Brak daty: samouwielbienie.
Oto dane w formie tabelarycznej:
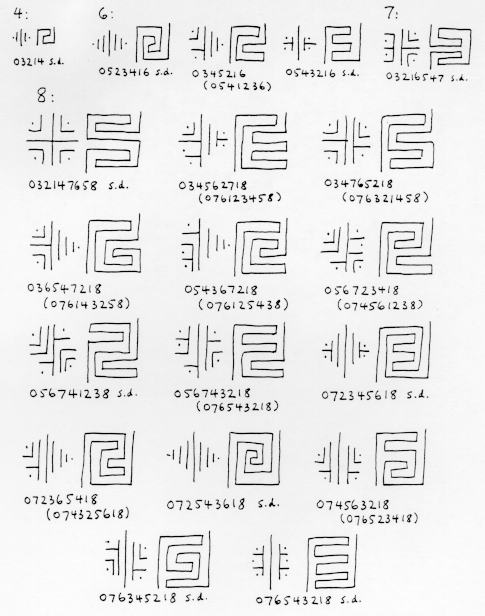
Głębokość   Liczba labiryntów    Ciekawe labirynty

  1              1                 żaden

  2              1                 żaden

  3              1                 żaden

  4              2                03214

  5              3                 żaden

  6              8          0523416   0543216
                            0345216   0541236

  7             14               03216547 

  8             42   032147658   034567218   034765218 
                     036547218   054367218   056723418 
                     056741238   056743218   072345618  
                     072365418   072543618   074325618 
                     074561238   074563218   076123458 
                     076125438   076143258   076321458 
                     076345218   076523418   076541238 
                     076543218

Dla głębokości 9 należałoby wziąć pod uwagę 24 x 24 = 576 permutacji i zwiększyć możliwości błędu. Poniższe liczby zostały obliczone za pomocą komputerów.

                    n           M(n)        I(n)
                    1             1          0 
                    2             1          0 
                    3             1          0 
                    4             2          1
                    5             3          0 
                    6             8          4 
                    7            14          1 
                    8            42         22 
                    9            81         11   
                   10           262        142  
                   11           538         95  
                   12          1828       1014 
                   13          3926        808   
                   14         13820       7796
                   15         30694       6980    
                   16        110954      63386    
                   17        252939      61725   
                   18        933458     538534  
                   19       2172830     558853    
                   20       8152860    4740658    
                   21      19304190    5171300    
                   22      73424650   42969130

                   24     678390116

                   26    6405031050 

                   28   61606881612 

                   30  602188541928

                   32 5969806669034

Tutaj M(n) i I(n) to liczba labiryntów i interesujących labiryntów głębokości n. Wartości dla 24, 26 i 28 zostały uzyskane przez Jima Reeds z Bell Labs metodą, która wydaje się nie mieć zastosowania do nieparzystych liczb głębokości. Wartości 30 i 32 podano w Lando and Zvonkin za 1993 papierze jako powodu V.R. Pratt.

Interesujące 9-poziomowe labirynty są pokazane na tej figurze poprzez ich prostokątne ścieżki labiryntu; znowu losowany jest tylko jeden przedstawiciel każdej pary podwójnej.