This is the translation. The original web-page (oryginalna strona): https://nstarr.people.amherst.edu/trom/intro.html
autor: Norton Starr
O układance – fizycznej i wirtualnej
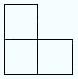
 Podstawowa łamigłówka składa się z 21 pionowych elementów („kafelków”) pokazanego rodzaju, złożonych z trzech kwadratów; jedna dodatkowa pojedyncza kwadratowa płytka; oraz płaszczyzna, siatka kwadratowa 8*8, której kwadraty są tego samego rozmiaru co kwadraty płytek. Płytki zajmują łącznie 3*21 + 1 = 63 + 1 = 64 kwadratów, tyle samo kwadratów co na szachownicy. W dalszej części nazywamy te ukośne elementy triominy, jako najprostszą z kilku nazw używanych do nich, które obejmują L-triominy, L-triominy i V-triominy.
Podstawowa łamigłówka składa się z 21 pionowych elementów („kafelków”) pokazanego rodzaju, złożonych z trzech kwadratów; jedna dodatkowa pojedyncza kwadratowa płytka; oraz płaszczyzna, siatka kwadratowa 8*8, której kwadraty są tego samego rozmiaru co kwadraty płytek. Płytki zajmują łącznie 3*21 + 1 = 63 + 1 = 64 kwadratów, tyle samo kwadratów co na szachownicy. W dalszej części nazywamy te ukośne elementy triominy, jako najprostszą z kilku nazw używanych do nich, które obejmują L-triominy, L-triominy i V-triominy.
Aby odtworzyć fizyczną wersję tej układanki, używając 21 rzeczywistych płytek tromino pojedynczy kwadratowy kawałek, a 8*8 szachownicy-like podstawy, pierwszej pozycji pojedynczej płytki kwadratowe na jednego z 64 miejsc kwadratowych w podstawie. Następnie należy wypełnić pozostałe 63 kwadraty z tych trominoes tak, że nie ma i nie pokrywają się niewypełnione kwadratowy. Takie rozwiązanie zagadki jest nazywany dachówka z 8*8 kwadratu. Alternatywnie, najpierw kolejno umieszczenie trominoes do podstawy szachownicy (każdy taki płytki zajmują jedynie trzy pola wzoru siatki), i gdy wszystkie 21 są umieszczone, umieścić jedną kwadratową płytkę w jednej pozycji, że są one dostępne.
Oto tło do wersji komercyjnej tej układanki, sprzedawany przez Kadon Enterprises. W styczniu 2000 dorocznym spotkaniu Towarzystwa Matematycznego Ameryki, Arthur Benjamin otrzymał nagrodę Haimo za wybitne nauczania uczelni. W swojej mowie dziękczynnej naszkicował swój ulubiony dowód przez indukcję. Takie rozumowanie zapewnia, że 2n*2n jednokomórkowego kwadratowy (czyli uogólnione szachownica z 2n kwadraty wzdłuż każdego boku) z jednej komórki zajętej, zawsze mogą być wyłożone przez trominoes. Trzy lata po wysłuchaniu uwag Benjamina Dawałem wykład na temat indukcji i przypomniał jego ulubiony dowód. Uzupełnienie moje przygotowanych przykładów mogę ad libbed klasyczny argument, ze względu na Solomona Golomb. Myśląc, że rzeczywiste logiczna tego rodzaju byłoby dodać element rzeczywistości i może wzbudzić zainteresowanie metodą indukcji, wysłałem list do Kadon, Wiodący ekspres puzzle, aby zobaczyć, czy mają każdy mógł ja zakupić. Nie zrobili, więc zapytałem, czy robią niektórzy moim przeznaczeniem. Seria e-maile z Kate Jones, prezes Kadon doprowadziło do układanki rodzaju ilustrowany powyżej lewo. Zasugerowała przy użyciu kilku różnych kolorów dla płytek tromino, dzięki czemu jest bardziej interesującą zagadkę niż pierwotnie przewidywał. Zdecydowałem się na chłodnicy, półprzezroczysty rozmieszcza zamiast odważnych, nieprzezroczyste te i wybrał niebieski, jasnoniebieski i ametyst dla trominoes.
Kate zapytał, czy chciałbym niech Kadon dodać zagadkę do tablicy elementów sprzedają i ja chętnie się zgodził – Chciałem tylko trochę dla własnego użytku. Ku mojemu zaskoczeniu, oświadczyła, że będę otrzymywać tantiemy. Że nigdy nie było moim celem, a wszystkie moje tantiemy są oddawane do Amherst College i Stowarzyszenie matematyczne Ameryki.
Kadon przyniósł zagadkę pod nazwą „Vee-21”; zobacz www.gamepuzzles.com/polycub2.htm#V21. Ta komercyjna wersja, w trzech żywych, półprzezroczystych kolorach akrylowych, zawiera czterdziestostronicową broszurę zawierającą szereg ulepszeń podstawowej układanki. Kate przyczyniła się do pewnych rozszerzeń układanki, niektórych dwuosobowych gier strategicznych oraz sugestii dotyczących wymagań dotyczących separacji kolorów dla przechyleń, które można by spróbować. Odkryła także możliwości estetyczne tworzenia symetrycznych wzorów. Kate zaprosiła Oriela Maxima do wzięcia udziału w swoich labiryntowych wyzwaniach związanych z układaniem kafelków za pomocą puzonów, a broszura zawiera różnorodne prostokątne szablony ze strategicznie dobranymi liniami siatki przyciemnionymi, aby służyły jako bariery, przez które puzony nie mogą być stawiane.
Dwa interaktywne łamigłówki komputerowe tego typu przewidziane są tutaj. 8-przez-8 puzzle został opracowany przez dwóch moich studentów, podczas gdy kolega resortowych przyczyniły M-by-N puzzle. Puzzle M-by-N (gra na większości systemów, ale może być wolny od obciążenia) jest nieco bardziej elastyczne, co pozwala na wybór dowolnej liczby wierszy i kolumn od 2 do 32 włącznie. Puzzle 8-na-8 (gra najlepiej z Internet Explorer na komputerze) ma inne działanie myszy i użytecznie ograniczona do trzech kolorach tromino. Wskazówki są podane ze sobą. Wersje online i Kadon oba mają niezwykłe wszerz odwołania intrygujące dla czterech latków, jak i doświadczonych puzzlers.
Historia
Dowód, że dla każdej liczby całkowitej n, 2n*2n kwadrat z jednej komórki zajęte (jest „niedobór” kwadrat), zawsze mogą być układana jak płytki trominoes wynika Solomona Golomb. Wydał go w 1954 roku artykule [9] w Amerykańskim Miesięcznik Matematyczny. Jak wspomniano powyżej, to w celu zilustrowania argumentu Golomb dla 2n*2n niedoborem kwadratów, że logiczna została uruchomiona. Jego sam artykuł wprowadzono drukować termin tromino i jego uogólnienie Polyomino, Polyomino jest podłączony szereg jednakowych pól mających tę właściwość, że dowolne dwa kwadraty albo nie stykają się, albo stykają się wzdłuż całej, wspólnej krawędzi. Tylko dwa kształty tromino są trzy pola w rzędzie i kształt litery L tej logiczne, a tu „tromino” odnosi się jedynie do tych ostatnich.
Dowód Golomb jest przykładem pierwszego stopa indukcji matematycznej. Oprócz czystej elegancji argumentu, to rzadki przypadek z nonnumerical stosowania tego sposobu. Stoi to w przeciwieństwie do przykładów i ćwiczeń, często znajdując się w zabiegach podręcznikowych indukcji, które zwykle składają się z różnych wzorów na skończonych sum, nierówności, i tym podobne. Dowodem na pierwszy występ w popularnym ośrodku była Josepha Madachy za Rekreacyjny magazyn matematyczny (RMM), gdzie Golomb wliczone go w pierwszym z jego czterech części serii artykułów na polyominoes opublikowane w Kontroli ryzyka [10]. W Martina Gardnera nasiennego maja 1957 Amerykański naukowiec Kolumna wprowadzenie polyominoes do szerszej publiczności, zauważył, że „płyta z jednego kwadratu brakuje w każdym momencie może zostać objęty 21 Prawo trominoes” [6, s. 154]. Na swojej pierwszej książki zebranych Gry matematyczne kolumn, Gardner opracowany przez zauważając, że „genialny indukcja argumentu pokazuje, że 21 Prawo trominoes i jeden monomino obejmie płytę 8-na-8, niezależnie od tego, gdzie monomino umieszcza” [8, s. 126].
Argument tromino Dachówka dla niedoborem szachownice i ogólnym 2n*2n twierdzenie pojawiła się w kolejnych książkach od czasu Miesięczny i RMM artykułów. Wyjaśniono w klasycznych Golomb za Polyominoes [11, 1965, s. 21-22], a w drugim wydaniu tej książki [11, 1994, s. 5]. Druga edycja daje bogatą historię i bogaty przegląd tego intrygującego tematu, i jest wypełniona zdjęć i łamigłówki. Jej 22 stron odniesienia, powołując się zarówno książki i artykuły są dodatkowym bonusem. Indeks listach nazwiska 81 osób, sporo mowa częściej niż raz w treści książki. Wiele z nich zostaną uznane przez miłośników gier i amatorów matematyków, jak również przez specjalistów w każdej dziedzinie. Opis książki podano w przeglądzie [17] George Martina. W 1976 roku Ross Honsberger dał świadomy, szczegółowe stosowanie argumentu Golomb dla rady sprawdzania jego Matematycznego Klejnoty II [13, s. 61]. Podstawową ideą dowodu również wspomniane w książce George E. Martin poświęcona tilings Polyomino [16, s. 27-28]. David Singmastera opinię [22] od tej ostatniej książki jest szczególnie interesujący, gdyż daje piękny szkic przedmiotu i jego historii.
Ten wątek jest również coraz bardziej powszechne taryfy dla tekstów i książek problemowych. Przykładowo, wydaje się, w dyskretnych matematyki tekstów Susanna Epp [5, str. 234], Richard Johnsonbaugh (który wymienia tromino tilings prostokątów za powstałe w VLSI projektowania układu) [14, s. 58-59], a Kenneth Rosen [20, str. 247-8]. Tromino Dachówka jest również traktowane w książce Daniela Velleman chodzi o dowody budujących [26, s. 271-275] oraz książek problem przez Johna P. D’Angelo i Douglas B. Zachodzie [1, s. 75] i Jiř Herman Radan Kučera i Jaromr IMA [12, str. 271]. Najbardziej krystaliczny ilustracja argumentu Golomb jest zamienna „Dowód bez słów” Roger Nelsen za podane w swojej drugiej książce z tego tytułu [19, s. 123].
Ten obszar matematyki rekreacyjnych skorzystał z ciągłym strumieniem dochodzenia i sugerowanych problemów. W latach 1985 i 1986, to Ping Chu i Richard Johnsonbaugh badane kwestii płytki niedoborem nn desek, w którym n nie musi być potęgami 2, a bardziej ogólnie, niewystarczająca i nie pozbawione prostokątne deski [3, 4 ]. Książka George’a Martina włączone cały rozdział poświęcony tromino tilings [16, s. 23-37]. Problemy zabarwienie dla tromino kafli są traktowane przez Ilvars Mizniks, który przyznaje, kolor strony wyboru Kadon Vee-21 jako inspiracji dla jego badań [18]. W 2004 roku artykuł [2] J. Ash Marshall i Salomona Golomb około tromino płytek niedoboru prostokątów zawiera wiele nowych i podstawowych danych, z których jeden odpowiada na starą pytanie Chu i Johnsonbaugh. Popiół i Golomb koniec z otwartą problemu około 2 niedoborem prostokątów (prostokąty z dwóch komórek usunięte).
Internet jest dobrym źródłem kafelków wyświetlaczy i informacji. Na przykład wyszukiwanie „tromino” i „kafelkowanie” powoduje, że aplety takie jak Alexander Bogomolny z www.cut-the-knot.org/Curriculum/Games/TrominoPuzzle.shtml i Christopher Mawata w www.utc.edu/Faculty/Christopher-Mawata/trominos/, które ilustrują puzzle tromino o różnych rozmiarach.
Wariacje
Oto niektóre rozszerzenia układanki tromino które mogłyby rozważyć czytelników. Pierwszy został zaproponowany przez mojego brata Raymonda (Pete), który zapytał, jak można by zorganizować trominoes w siatce 8*8, tak aby zmaksymalizować liczbę pustych kwadraty. Można to szerzej: jedna droga ośmieliłbym płytek i siatki są listwą więc pozostają one w miejscu, podczas gdy alternatywnie można pozwolić płytki przesuwać tak, aby umożliwić ściskanie w tak wielu płytek jak to możliwe (zawsze w linii siatki). Pete nie był świadomy, że wersja na rzep jest odmianą Pentomino pozycjonowania układanki Golomb jako opisane przez Gardnera [7, s. 128] i [8, s. 133]. Golomb rozszerzony zagadkę do dwuosobowej grze Pentomino [7, s. 128] i [8, str. 133-135] Zasady, które mogą być stosowane do układanki tromino również. David Klarner zgłaszać na Pentomino grze dwuosobowej, Pan-kai (opracowany przez Alex Randolph i wydany w 1961 roku przez Phillips Publishers), który obejmował następujące ograniczenia: Najważniejszą zasadą jest to, że zabrania się grać kawałek w zamkniętym obszarze płyty, jeśli mniej niż 5 komórek będzie wtedy pozostają nieobsadzone, chyba że ruch dokładnie wypełnia region. [15, s. 8] (patrz [21, str. 75] Więcej informacji na temat Randolph i Pan-kai).
Innym kierunkiem jest trójwymiarowy. Rozważmy sześcianu o długości boku 2n, zawierający 23n komórki jednostkowe, z których jeden jest zajęty (pojedynczy niedobór). Można pozostałe komórki są wyłożone trzech trominoes wymiarów (trzy kostki w kształcie litery L, a dwa z nich spełniająca trzeci na dwóch sąsiednich powierzchniach drugiego)? Niezbędnym warunkiem, że 2n = 3k + 1 okazuje się niewystarczające, oraz. [23, Rozdział 6: Norton Starrs 3-wymiarowy Tromino Okładziny], [24, pp 72-87.] I [25] przypadku 444 kostek przedstawia niektóre skromne wyzwań, które mogą bawić młodych łamigłówki.
Prostsze problemy łatwo sugerują się i zostały uznane przez wielu innych. Na przykład, można pełne 3*3 i 6*6 macierze kwadratowe są wyłożone trominoes? Czy każdy z niedoborem 5*5 i 7*7 kwadratowa tablica być wyłożone? Te dwa ostatnie puzzli są trudniejsze niż pełne 3*3, 6*6 i 8*8 z niedoborem przypadkach. Idąc dalej, czytelnik może rozważyć tilings różnych prostokątnymi tablicami – patrz poniższe odnośniki. W przypadku korzystania z wersji z więcej niż jednym kolorze tromino, takich jak Kadon Vee-21, należy rozważyć różne ograniczenia kolorów. Na przykład, spróbuj układając płytki, tak aby żadne dwa tego samego koloru akcję krawędź. W kierunku przeciwnym, spróbuj grupy jak wiele płytek ją razem koloru jak to możliwe. Dla obu tych typów sygnatur, próbować dalej, aby Dachówka pojawiać symetryczny o przekątnej lub wokół linii poziomej lub pionowej. Możliwości zabawy i odkrycia są liczne. Prostokątów różne wielkości mogą być badane przez kliknięcie M przez N puzzle. Dla kolorystycznych eksperymentów wzór, puzzle Kadon jest najlepszy.
Referencje
- JP D’Angelo i DB Zachód, Myślenia matematycznego: rozwiązywanie problemów i Dowody, drugie wydanie, Prentice Hall, Upper Saddle River, NJ, 2000.
- JM popiołu i SW Golomb „Układanie niedoborem prostokątów z trominoes” Magazyn Matematyki, 77 (2004), 46-55. (Dostępny w math.depaul.edu/~mash/TileRec3b.pdf)
- IP Chu i R. Johnsonbaugh „Układanie płyt z niedoborem trominoes” Magazyn Matematyki, 59 (1986), 34-40.
- IP Chu i R. Johnsonbaugh „Płytek ceramicznych płyt z trominoes” J. rekreacyjne Mat., 18 (1985/86), 188-193.
- SS EPP, Matematyka dyskretna z aplikacjami, wydanie trzecie, Thomson, Belmont, CA, 2004.
- M. Gardner, „O niezwykłym podobieństwem Grze Icosian i Wieża Hanoi” Amerykański naukowiec, 196, (maj 1957), 150-156. Kolumna ta była przede wszystkim poświęcona obwodów Hamilton, ale kończy się rozdział poświęcony szachownicy płytki problemów: Gardner twierdzi, że szachownica/domino problem „Kolumna lutowej poproszony Octave Levenspiel z Bucknell Uniwersytet zadzwonić moją uwagę na niezwykłą artykule SW Golomb w Amerykańskim Matematycznego miesięczny na grudzień 1954”
- M. Gardner, „Więcej o złożonych domina, plus odpowiedzi na zagadki w ubiegłym miesiącu,” Amerykański naukowiec, 197, (grudzień 1957), 126-140. To Gry matematyczne kolumn rozpoczyna się od zgłaszania wybuchową wpływ krótki rachunek Kolumna może w pracy Golomb [6]: „W roku, ponieważ dział ten został zainaugurowany, że otrzymał więcej listów o jednej matematycznej rekreacji niż jakakolwiek inna z«Pentomino» Problem Setki korespondentów wysłanych w bardzo różnych rozwiązań. Wiele świadczy o problemie dziwne fascynacji„.
- M. Gardner, Amerykański naukowiec Książka zagadek matematycznych i różnorodności, Simon and Schuster, New York, 1959 (przedruk i aktualizowany Sześciokąty i innych matematycznych różnorodności, University of Chicago Press, 1988) [rozdział 13 niniejszego pierwszej takiej kolekcji łączy materiału płytki z [6], [7], a pod tytułem „Polyominoes”].
- SW Golomb „Szachownica Tablice i Polyominoes,” Amer. Mat. Miesięczny, 61 (1954), 675-682.
- SW Golomb „Ogólna teoria poliominoów Część I – Domino, Pentominoes i szachownice” Rekreacyjny magazyn matematyczny, Nr Wydanie 4 (sierpień 1961), 3-12.
- SW Golomb, Polyominoes, Scribner, New York, 1965 (drugie wydanie: Polyominoes, Puzzle, wzory, problemy i Opakowania, Princeton University Press, Princeton, 1994)
- J. Hermana, R. Kučera i J. ima, Liczenia i konfiguracjach: Problemy w Kombinatoryka, arytmetyka i geometria (Karl Dilcher, tłumacz), Springer-Verlag, New York, 2003.
- R. Honsberger, Matematyczna Klejnoty II , Stowarzyszenie matematyczne Ameryki, Washington, DC, 1976.
- R. Johnsonbaugh, Matematyka dyskretna, szóste wydanie, Pearson Prentice Hall, Upper Saddle River, NJ, 2005.
- D. Klarner, Pudełko-Pakowanie puzzle. Notatki Multilithed, University of Waterloo, Ontario, 1973/74. 42 + strony tytułowej. (Część tej zestawiono w rozdziale 8 Honsberger [13]).
- GE Martin, Polyominoes, Przewodnik zagadki i problemy w Posadzki, Stowarzyszenie matematyczne Ameryki, Washington, DC, 1991.
- GE Martin, przegląd S. Golomb za Polyominoes (1994 Edition), Recenzje matematyczne, MR1291821 (95 kB: 00006), 1995.
- I. Mizniks, „Komputer Analiza 3 kolor problemem dla V-Shapes”, Acta Societatis Mathematicae Latviensis, Streszczenia 5. Konferencji łotewski Matematycznego, kwiecień 6-7, 2004, Daugavpils, Łotwa. (Dostępny w http://www.de.dau.lv/matematika/lmb5/tezes/Mizniks.pdf)
- RB Nelsen, Dowody bez słów II, więcej ćwiczeń w programie Myślenie wizualne, Stowarzyszenie matematyczne Ameryki, Washington, DC, 2000.
- KH Rosen, Matematyka dyskretna i jej zastosowań, wydanie piąte, McGraw-Hill, New York, 2003. (Żeby ukazać jak w przykładzie 13, pkt 4.1, w szóstej edycji 2007.)
- JN Silva (Ed.) Rekreacyjny Matematyka Kolokwium I (Materiały konferencyjne, 29 kwietnia-2 maja 2009. Uniwersytet Évora), Associação Ludus, Lisboa, 2010.
- D. Singmaster, przegląd GE Martina Polyominoes, restauracjach Matematycznych, MR1140005 (93D: 00006), 1993.
- A. Soifer, Geometria Etudes w Combinatorial Matematyki, wydanie drugie, Springer, New York, 2010.
- N. Starr, Tromino Okładziny Nieskuteczne kostki o boku długości 2n, Geombinatorics XVIII (2) (2008), 72-87.
- N. Starr, Tromino Okładziny niedoborem Kostki dowolnej długości boku, http://arxiv.org/abs/0806.0524, 3 czerwca 2008 roku.
- DJ Velleman, Jak to udowodnić: uporządkowane podejście, wydanie drugie, Cambridge University Press, New York, 2006
© 2012 Norton Starr